Quantitative : Discrete, Continuous
Referred to as numeric, Quantitative data have two types: Discrete and Continuos. Continuous are measurement and discrete are counts, as a general rule.
A count that can't be made precise more is discrete data. It involves integers typically. It is a discrete data which is the number of children (or pets, or adults), for instance, the reason is whole are counting by yourself, entities indvisible: 1.3 pets or 2.5 kids, you can't have it.
On the other hand, continuos data, to finer and finer levels it could reduce and could be divided. For examlple, at progressively more precise - beyond, milimiters, centimeters and meters - so height are continuos data.
Qualitative
Qualitative data is characterizes or approximates by data but properties, attributes, characteristics, etc are not measured, of phenomenon or a thin. Whereas quantitative data defines is where qualitative data describes.
My Mathematics Blog
Wednesday, 13 July 2016
Measures of dispersion
Standard Deviation
Within a set of data, a measure of the spread of scores are the standard deviation defines.
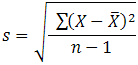
where,
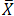 = sample mean
= sample mean
n = number of scores in sample.
s = sample standard deviation
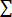 = sum of...
= sum of...
Within a set of data, a measure of the spread of scores are the standard deviation defines.
Formulas for the standard deviation
Sample standard deviation formula is: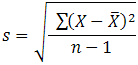
where,
n = number of scores in sample.
s = sample standard deviation
Measures of central tendency
Mean:
-- The mean is found when the numbers of data entries dividing and adding up all of the given data. It is also known as the average.
Example:
- the grades were as follows, the class of grade 110 math had a mathematics test recently:
78
66
82 464 / 6 = 77.3
89
75 Hence, the mean average of the class is 77.3.
+ 74
464
Median:
-- The middle number is the median. First you arrange the numbers in order from lowest. Firstly, from the lowest, in order you arrange the numbers
to highest, by crossing off the numbers until you reach the
middle then you find the middle number.
Example:
- to find the median, use the above data:
66 74 75 78 82 89\
- There is no middle number, as you can see we have two numbers What should we do?
find the average and we take the two middle numbers , ( or mean ). It is simple;
75 + 78 = 153
153 / 2 = 76.5
Hence, 76.5 is the middle number.
Mode:
-- this is the number that most often occurs.
Example:
- the following data below, find the mode:
78 56 68 92 84 76 74 56 68 66 78 72 66
65 53 61 62 78 84 61 90 87 77 62 88 81
78 is the Mode.
-- The mean is found when the numbers of data entries dividing and adding up all of the given data. It is also known as the average.
Example:
- the grades were as follows, the class of grade 110 math had a mathematics test recently:
78
66
82 464 / 6 = 77.3
89
75 Hence, the mean average of the class is 77.3.
+ 74
464
Median:
-- The middle number is the median. First you arrange the numbers in order from lowest. Firstly, from the lowest, in order you arrange the numbers
to highest, by crossing off the numbers until you reach the
middle then you find the middle number.
Example:
- to find the median, use the above data:
66 74 75 78 82 89\
- There is no middle number, as you can see we have two numbers What should we do?
find the average and we take the two middle numbers , ( or mean ). It is simple;
75 + 78 = 153
153 / 2 = 76.5
Hence, 76.5 is the middle number.
Mode:
-- this is the number that most often occurs.
Example:
- the following data below, find the mode:
78 56 68 92 84 76 74 56 68 66 78 72 66
65 53 61 62 78 84 61 90 87 77 62 88 81
78 is the Mode.
Sets and Venn Diagram
At the left shows overlap of two sets A and B of the Venn diagram. U is the universal set. In the center region labeled where the circles overlap is where the values that belong to both set A and set B are located. "Intersection" of the two sets is the region are called.

Videos of Shading regions Venn Diagrams
(Can only be played at google chrome)
Videos of Shading regions Venn Diagrams
(Can only be played at google chrome)
Geometric Progression
Geometric Progression, Series & Sums
Introduction
A geometric sequence is a sequence such that any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r. The common ratio (r) is obtained by dividing any term by the preceding term, i.e.,| where | r | common ratio |
| a1 | first term | |
| a2 | second term | |
| a3 | third term | |
| an-1 | the term before the n th term | |
| an | the n th term |
For example, the sequence 1, 3, 9, 27, 81 is a geometric sequence. Note that after the first term, the next term is obtained by multiplying the preceding element by 3.
The geometric sequence has its sequence formation:
To find the nth term of a geometric sequence we use the formula:
| where | r | common ratio |
| a1 | first term | |
| an-1 | the term before the n th term | |
| n | number of terms |
Arithmetic Progression
Arithmetic Progression
An arithmetic progression is a sequence of numbers such that the difference of any two successive members is a constant.For example, the sequence 1, 2, 3, 4, ... is an arithmetic progression with common difference 1.
Second example: the sequence 3, 5, 7, 9, 11,... is an arithmetic progression
with common difference 2.
Third example: the sequence 20, 10, 0, -10, -20, -30, ... is an arithmetic progression
with common difference -10.
Notation
We denote by d the common difference.By an we denote the n-th term of an arithmetic progression.
By Sn we denote the sum of the first n elements of an arithmetic series.
Arithmetic series means the sum of the elements of an arithmetic progression.
Properties
a1 + an = a2 + an-1 = ... = ak + an-k+1
and
an = ½(an-1 + an+1)
Sample: let 1, 11, 21, 31, 41, 51... be an arithmetic progression.
51 + 1 = 41 + 11 = 31 + 21
and
11 = (21 + 1)/2
21 = (31 + 11)/2...
If the initial term of an arithmetic progression is a1 and the common difference of successive members is d, then the n-th term of the sequence is given by
an = a1 + (n - 1)d, n = 1, 2, ...
The sum S of the first n numbers of an arithmetic progression is given by the formula:
S = ½(a1 + an)n
where a1 is the first term and an the last one.
or
S = ½(2a1 + d(n-1))n
Number Pattern
(can only be played in google chrome)
Pattern or a certain sequence that are followed by a list of numbers.
For Example: tarts at 1 and jumps 3 every time... 1, 4, 7, 10, 13, 16,
Another Example: doubles each time ... 2, 4, 8, 16, 32
(can only be played in google chrome)
Pattern or a certain sequence that are followed by a list of numbers.
For Example: tarts at 1 and jumps 3 every time... 1, 4, 7, 10, 13, 16,
Another Example: doubles each time ... 2, 4, 8, 16, 32
Subscribe to:
Comments (Atom)